Transformasi Lorentz awalnya hasil dari upaya oleh Lorentz dan orang lain untuk menjelaskan bagaimana kecepatan cahaya diamati untuk menjadi independen dari kerangka acuan, dan untuk memahami simetri hukum elektromagnetisme. Albert Einstein kemudian kembali diturunkan transformasi dari nya dalil-dalil relativitas khusus. Transformasi Lorentz menggantikan transformasi Galilea fisika Newton, yang menganggap mutlak sebuah ruang dan waktu. Menurut relativitas khusus, ini adalah pendekatan yang baik hanya pada kecepatan relatif jauh lebih kecil daripada kecepatan cahaya.
Jika ruang yang homogen , maka transformasi Lorentz harus menjadi transformasi linear.Juga, karena relativitas mendalilkan bahwa kecepatan cahaya adalah sama untuk semua pengamat, harus memelihara interval ruang-waktu antara dua peristiwa di ruang Minkowski .Transformasi Lorentz hanya menggambarkan transformasi di mana ruang-waktu di acara asal dibiarkan tetap, sehingga mereka dapat dianggap sebagai rotasi hiperbolik dari ruang Minkowski . Jenderal menetapkan lebih dari transformasi yang juga mencakup terjemahan ini dikenal sebagai kelompok Poincaré .
Transformasi Lorentz untuk frame dalam konfigurasi standar
Asumsikan ada dua pengamat O dan Q, masing-masing menggunakan sendiri sistem koordinat Cartesian untuk mengukur dan waktu interval ruang. menggunakan O (t, x, y, z) dan Q menggunakan (t ', x', y ', z') . Asumsikan lebih lanjut bahwa sistem koordinat yang berorientasi sehingga sumbu-x dan x '-sumbu adalah kesegarisan , y-axis sejajar dengan y '-sumbu, begitu juga sumbu-z dan'-z sumbu. Kecepatan relatif antara dua pengamat adalah v sepanjang sumbu x umum. Juga menganggap bahwa asal-usul kedua sistem koordinat yang sama. Jika semua terus ini, maka sistem koordinat dikatakan dalam konfigurasi standar. Sebuah presentasi simetris antara depan Lorentz Lorentz Transformasi dan Transformasi invers dapat dicapai jika sistem koordinat dalam konfigurasi simetris . Bentuk simetris menyoroti bahwa semua hukum fisika harus sedemikian jenis yang bahwa mereka tetap tidak berubah dalam transformasi Lorentz.
Transformasi Lorentz untuk frame dalam konfigurasi standar dapat terbukti:
mana  disebut faktor Lorentz .
disebut faktor Lorentz .
 disebut faktor Lorentz .
disebut faktor Lorentz .Formulir Matrix
Transformasi Lorentz disebut "meningkatkan" dalam arah-x dan seringkali dinyatakan dalam matriks bentuk sebagai
Matriks transformasi ini bersifat universal untuk semua empat - vektor.
Lebih umum untuk dorongan ke segala arah sewenang-wenang (β x, β y, z β),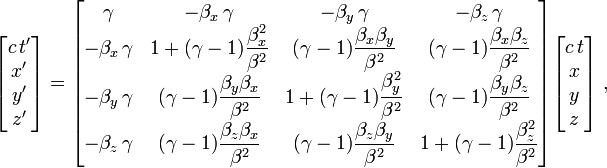
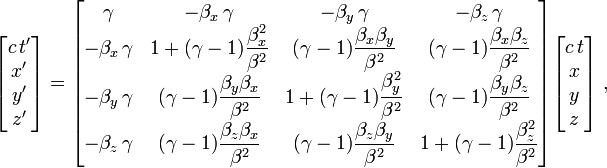
mana  dan
dan  .
.
 dan
dan  .
. Perhatikan bahwa transformasi ini hanya "meningkatkan," yaitu, transformasi antara dua frame yang x, y, dan z sumbu sejajar dan yang asal bertepatan ruang-waktu (lihat "Standar Konfigurasi" Gambar). Transformasi Lorentz yang tepat yang paling umum juga berisi rotasi tiga sumbu, karena komposisi dua meningkatkan bukan dorongan murni tetapi merupakan dorongan diikuti oleh rotasi.Rotasi menimbulkan presesi Thomas . meningkatkan ini diberikan oleh matriks simetris , tetapi matriks transformasi Lorentz umum tidak perlu simetris.
Komposisi dari dua Lorentz meningkatkan B (u) dan B (v) u kecepatan dan v diberikan oleh:
![B (\ mathbf {u}) B (\ mathbf {v}) = B (\ mathbf {u} \ oplus \ mathbf {v}) Gyr [\ mathbf {u}, \ mathbf {v}] = Gyr [\ mathbf {u}, \ mathbf {v}] B (\ mathbf {v} \ oplus \ mathbf {u})](http://upload.wikimedia.org/math/8/4/7/8475fe37698786b278628608804bfc29.png) ,
,
mana u  v adalah kecepatan-tambahan , dan Gyr [u, v] adalah rotasi yang timbul dari komposisi, gyr menjadi gyrovector ruang abstraksi dari presesi Thomas gyroscopic, dan B (v) adalah matriks 4x4 yang menggunakan komponen v, yaitu v 1, v 2, v 3 dalam entri dari matriks, atau lebih tepatnya komponen v / c dalam representasi yang digunakan di atas.
v adalah kecepatan-tambahan , dan Gyr [u, v] adalah rotasi yang timbul dari komposisi, gyr menjadi gyrovector ruang abstraksi dari presesi Thomas gyroscopic, dan B (v) adalah matriks 4x4 yang menggunakan komponen v, yaitu v 1, v 2, v 3 dalam entri dari matriks, atau lebih tepatnya komponen v / c dalam representasi yang digunakan di atas.
 v adalah kecepatan-tambahan , dan Gyr [u, v] adalah rotasi yang timbul dari komposisi, gyr menjadi gyrovector ruang abstraksi dari presesi Thomas gyroscopic, dan B (v) adalah matriks 4x4 yang menggunakan komponen v, yaitu v 1, v 2, v 3 dalam entri dari matriks, atau lebih tepatnya komponen v / c dalam representasi yang digunakan di atas.
v adalah kecepatan-tambahan , dan Gyr [u, v] adalah rotasi yang timbul dari komposisi, gyr menjadi gyrovector ruang abstraksi dari presesi Thomas gyroscopic, dan B (v) adalah matriks 4x4 yang menggunakan komponen v, yaitu v 1, v 2, v 3 dalam entri dari matriks, atau lebih tepatnya komponen v / c dalam representasi yang digunakan di atas.Komposisi dari dua transformasi Lorentz L (u, U) dan L (v, V) yang meliputi rotasi U dan V diberikan oleh:
Jika bentuk matriks 3x3 rotasi yang diterapkan untuk koordinat spasial diberikan oleh] gyr [u, v, maka matriks rotasi 4x4 diterapkan untuk 4-koordinat diberikan oleh:
![Gyr [\ mathbf {u}, \ mathbf {v}] = \ begin {pmatrix} 1 & 0 \ \ 0 & gyr [\ mathbf {u}, \ mathbf {v}] \ end {pmatrix}](http://upload.wikimedia.org/math/3/8/3/3834c8bfe18b5ab1078780cebd3c5779.png) .
.
Untuk meningkatkan dalam arah yang sewenang-wenang dengan kecepatan  , Akan lebih mudah untuk
, Akan lebih mudah untuk
 , Akan lebih mudah untuk
, Akan lebih mudah untuk Transformasi Lorentz
Jika  negatif, maka kami menetapkan
negatif, maka kami menetapkan  yang menjadi kecepatan invarian , dengan kecepatan cahaya dalam ruang hampa. Ini menghasilkan
yang menjadi kecepatan invarian , dengan kecepatan cahaya dalam ruang hampa. Ini menghasilkan  dan dengan demikian kita mendapatkan relativitas khusus dengan transformasi Lorentz
dan dengan demikian kita mendapatkan relativitas khusus dengan transformasi Lorentz
dimana kecepatan cahaya adalah konstan terbatas universal menentukan kecepatan tertinggi relatif mungkin antara frame inertial.
Jika 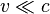 transformasi Galilea adalah pendekatan yang baik dengan transformasi Lorentz.
transformasi Galilea adalah pendekatan yang baik dengan transformasi Lorentz.
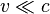 transformasi Galilea adalah pendekatan yang baik dengan transformasi Lorentz.
transformasi Galilea adalah pendekatan yang baik dengan transformasi Lorentz.Hanya percobaan dapat menjawab pertanyaan mana dari dua kemungkinan, κ = 0 atau κ <0, diwujudkan di dunia kita. Percobaan mengukur kecepatan cahaya, pertama kali dilakukan oleh seorang fisikawan Denmark Ole Rømer, menunjukkan bahwa itu adalah terbatas, dan percobaan Michelson-Morley menunjukkan bahwa kecepatan mutlak, dan dengan demikian bahwa κ <0.menguraikan vektor spasial 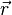 menjadi komponen-komponen tegak lurus dan sejajar dengan kecepatan
menjadi komponen-komponen tegak lurus dan sejajar dengan kecepatan  :
: 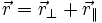 . Maka hanya komponen
. Maka hanya komponen  ke arah
ke arah  adalah 'menyesatkan' oleh faktor gamma:
adalah 'menyesatkan' oleh faktor gamma:
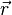 menjadi komponen-komponen tegak lurus dan sejajar dengan kecepatan
menjadi komponen-komponen tegak lurus dan sejajar dengan kecepatan  :
: 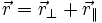 . Maka hanya komponen
. Maka hanya komponen  ke arah
ke arah  adalah 'menyesatkan' oleh faktor gamma:
adalah 'menyesatkan' oleh faktor gamma:dimana sekarang 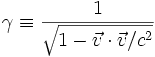 . Yang kedua ini dapat ditulis sebagai:
. Yang kedua ini dapat ditulis sebagai:
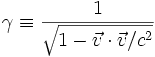 . Yang kedua ini dapat ditulis sebagai:
. Yang kedua ini dapat ditulis sebagai:Persamaan ini dapat dinyatakan dalam bentuk matriks sebagai
dimana I adalah matriks identitas, v adalah kecepatan ditulis sebagai vektor kolom, T v adalah transpos nya (vektor baris) dan  adalah versor nya.
adalah versor nya.
 adalah versor nya.
adalah versor nya.
Kecepatan
Transformasi Lorentz dapat dicetak ke dalam bentuk lain yang berguna dengan menetapkan parameter  disebut kecepatan sehingga,
disebut kecepatan sehingga,
 disebut kecepatan sehingga,
disebut kecepatan sehingga,dan
Dipersamakan:
Kemudian transformasi Lorentz dalam konfigurasi standar adalah:
Ekspresi trigonometri hiperbolik
Dari ekspresi di atas untuk φ e dan e-φ
dan karena itu,
Rotasi koordinat hiperbolik
Mengganti ekspresi tersebut ke dalam bentuk matriks transformasi, kita memiliki:
Dengan demikian, transformasi Lorentz dapat dilihat sebagai hiperbolik rotasi koordinat di ruang Minkowski, di mana φ kecepatan merupakan hiperbolik sudut rotasi.
Ruang-waktu selang
Dalam sistem koordinat tertentu (x μ), jika dua peristiwa A dan B yang dipisahkan oleh
dengan interval ruang-waktu antara mereka diberikan oleh
Hal ini dapat ditulis dalam bentuk lain menggunakan metrik Minkowski . Dalam sistem koordinat,
Kemudian, kita dapat menulis
atau, menggunakan konvensi penjumlahan Einstein ,
Sekarang anggaplah bahwa kita membuat sebuah transformasi koordinat  . Kemudian, interval dalam sistem koordinat diberikan oleh
. Kemudian, interval dalam sistem koordinat diberikan oleh
 . Kemudian, interval dalam sistem koordinat diberikan oleh
. Kemudian, interval dalam sistem koordinat diberikan olehatau
Ini adalah hasil dari relativitas khusus yang interval adalah invarian . Artinya,  . Hal ini dapat ditunjukkan bahwa ini memerlukan koordinat transformasi untuk menjadi bentuk
. Hal ini dapat ditunjukkan bahwa ini memerlukan koordinat transformasi untuk menjadi bentuk
 . Hal ini dapat ditunjukkan bahwa ini memerlukan koordinat transformasi untuk menjadi bentuk
. Hal ini dapat ditunjukkan bahwa ini memerlukan koordinat transformasi untuk menjadi bentukDi sini, 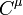 adalah vektor konstan dan
adalah vektor konstan dan  sebuah konstanta matriks, di mana kita mengharuskan
sebuah konstanta matriks, di mana kita mengharuskan
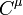 adalah vektor konstan dan
adalah vektor konstan dan  sebuah konstanta matriks, di mana kita mengharuskan
sebuah konstanta matriks, di mana kita mengharuskanTransformasi tersebut disebut transformasi Poincaré atau transformasi Lorentz homogen merupakan terjemahan ruang-waktu. Ketika  , Transformasi disebut transformasi Lorentz homogen, atau hanya sebuah transformasi Lorentz.
, Transformasi disebut transformasi Lorentz homogen, atau hanya sebuah transformasi Lorentz.
 , Transformasi disebut transformasi Lorentz homogen, atau hanya sebuah transformasi Lorentz.
, Transformasi disebut transformasi Lorentz homogen, atau hanya sebuah transformasi Lorentz.Mengambil penentu 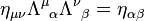 memberi kita
memberi kita
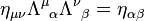 memberi kita
memberi kitaLorentz transformasi dengan  membentuk sebuah sub kelompok yang disebut transformasi Lorentz yang tepat yang merupakan ortogonal khusus kelompok S O (1,3). Mereka dengan
membentuk sebuah sub kelompok yang disebut transformasi Lorentz yang tepat yang merupakan ortogonal khusus kelompok S O (1,3). Mereka dengan  disebut transformasi Lorentz yang tidak benar yang tidak subkelompok, sebagai produk dari setiap dua transformasi Lorentz yang tidak benar akan menjadi sebuah transformasi Lorentz yang tepat. Dari definisi di atas Λ dapat ditunjukkan bahwa
disebut transformasi Lorentz yang tidak benar yang tidak subkelompok, sebagai produk dari setiap dua transformasi Lorentz yang tidak benar akan menjadi sebuah transformasi Lorentz yang tepat. Dari definisi di atas Λ dapat ditunjukkan bahwa  , Jadi baik
, Jadi baik  atau
atau  , Yang disebut orthochronous dan non-orthochronous masing-masing. Sebuah subkelompok penting dari transformasi Lorentz yang tepat adalah orthochronous tepat transformasi Lorentz yang terdiri murni meningkatkan dan rotasi. Setiap transformasi Lorentz dapat ditulis sebagai orthochronous yang tepat, bersama dengan satu atau kedua dari dua transformasi diskrit; inversi ruang (P) dan pembalikan waktu (T), yang non-zero unsur tersebut adalah:
, Yang disebut orthochronous dan non-orthochronous masing-masing. Sebuah subkelompok penting dari transformasi Lorentz yang tepat adalah orthochronous tepat transformasi Lorentz yang terdiri murni meningkatkan dan rotasi. Setiap transformasi Lorentz dapat ditulis sebagai orthochronous yang tepat, bersama dengan satu atau kedua dari dua transformasi diskrit; inversi ruang (P) dan pembalikan waktu (T), yang non-zero unsur tersebut adalah:
 membentuk sebuah sub kelompok yang disebut transformasi Lorentz yang tepat yang merupakan ortogonal khusus kelompok S O (1,3). Mereka dengan
membentuk sebuah sub kelompok yang disebut transformasi Lorentz yang tepat yang merupakan ortogonal khusus kelompok S O (1,3). Mereka dengan  disebut transformasi Lorentz yang tidak benar yang tidak subkelompok, sebagai produk dari setiap dua transformasi Lorentz yang tidak benar akan menjadi sebuah transformasi Lorentz yang tepat. Dari definisi di atas Λ dapat ditunjukkan bahwa
disebut transformasi Lorentz yang tidak benar yang tidak subkelompok, sebagai produk dari setiap dua transformasi Lorentz yang tidak benar akan menjadi sebuah transformasi Lorentz yang tepat. Dari definisi di atas Λ dapat ditunjukkan bahwa  , Jadi baik
, Jadi baik  atau
atau  , Yang disebut orthochronous dan non-orthochronous masing-masing. Sebuah subkelompok penting dari transformasi Lorentz yang tepat adalah orthochronous tepat transformasi Lorentz yang terdiri murni meningkatkan dan rotasi. Setiap transformasi Lorentz dapat ditulis sebagai orthochronous yang tepat, bersama dengan satu atau kedua dari dua transformasi diskrit; inversi ruang (P) dan pembalikan waktu (T), yang non-zero unsur tersebut adalah:
, Yang disebut orthochronous dan non-orthochronous masing-masing. Sebuah subkelompok penting dari transformasi Lorentz yang tepat adalah orthochronous tepat transformasi Lorentz yang terdiri murni meningkatkan dan rotasi. Setiap transformasi Lorentz dapat ditulis sebagai orthochronous yang tepat, bersama dengan satu atau kedua dari dua transformasi diskrit; inversi ruang (P) dan pembalikan waktu (T), yang non-zero unsur tersebut adalah:Himpunan transformasi Poincaré memenuhi sifat kelompok dan disebut kelompok Poincaré . Di bawah program Erlangen , Minkowski ruang dapat dilihat sebagai geometri didefinisikan oleh kelompok Poincaré, yang menggabungkan transformasi Lorentz dengan terjemahan. Dalam cara yang sama, himpunan semua transformasi Lorentz bentuk kelompok, yang disebut kelompok Lorentz .
Sebuah invarian kuantitas bawah transformasi Lorentz dikenal sebagai skalar Lorentz .
Ekspresi transformasi Lorentz
Menggunakan hubungan yang diperoleh sebelumnya
seseorang
dan, akhirnya
Kami sekarang memiliki semua koefisien diperlukan dan, oleh karena itu, transformasi Lorentz
![x = \ frac {x '+ vt'} {\ sqrt [] {1 - \ frac {v ^ 2} {c ^ 2}}}](http://upload.wikimedia.org/math/2/0/9/2097720541dcd5d6cb9a04487814d4ba.png)
![t = \ frac {t '+ \ frac {vx'} {c ^ 2}} {\ sqrt [] {1 - \ frac {v ^ 2} {c ^ 2}}}](http://upload.wikimedia.org/math/f/a/0/fa0a022eb43c916950ce61bc0f99fec8.png) ,
,
atau, menggunakan γ faktor Lorentz,
dan kebalikannya:
Relativitas khusus
Salah satu konsekuensi paling mengejutkan metode jam-setting Einstein adalah gagasan bahwa waktu adalah relatif. Pada intinya, setiap frame pengamat acuan dikaitkan dengan seperangkat unik jam, hasil yang waktu itu berlalu pada tingkat yang berbeda untuk pengamat yang berbeda. Ini adalah hasil langsung dari transformasi Lorentz dan disebut dilatasi waktu . Kita juga bisa dengan jelas melihat dari transformasi "waktu setempat" Lorentz bahwa konsep relativitas simultanitas dan relativitas kontraksi panjang juga konsekuensi dari hipotesis jam-setting.
transformasi Lorentz juga dapat digunakan untuk membuktikan bahwa medan magnet dan listrik hanya aspek yang berbeda dari gaya yang sama - gaya elektromagnetik. Jika kita memiliki satu muatan atau pengumpulan biaya yang semuanya stasioner dengan menghormati satu sama lain, kita dapat mengamati sistem dalam sebuah frame di mana tidak ada gerakan dari tuduhan. Dalam kerangka ini, hanya ada sebuah "medan listrik". Jika kita beralih ke bingkai bergerak, transformasi Lorentz akan memprediksi bahwa "medan magnet" hadir. Bidang ini awalnya disatukan dalam konsep Maxwell dari "medan elektromagnetik".
Penurunan
Perlakuan biasa (misalnya, karya asli Einstein) didasarkan pada sifat invarian dari kecepatan cahaya. Namun, ini belum tentu titik awal: memang (seperti terkena, misalnya, dalam volume kedua dari Kursus dari teori Fisika oleh Landau dan Lifshitz), apa yang sebenarnya yang dipertaruhkan adalah lokalitas interaksi: satu mengandaikan bahwa pengaruh yang satu partikel, misalnya, diberikan pada lain tidak dapat ditransmisikan secara instan. Oleh karena itu, ada kecepatan maksimal teoritis transmisi informasi yang harus invariant, dan ternyata bahwa kecepatan ini bertepatan dengan kecepatan cahaya dalam vakum. Kebutuhan lokalitas dalam teori fisika sudah dicatat oleh Newton (lihat Koestler "The berjalan dalam tidur"), yang menganggap gagasan dari suatu tindakan di kejauhan "filosofis masuk akal" dan percaya gravitasi yang harus ditularkan oleh agen (eter antar bintang) yang mematuhi hukum-hukum fisik tertentu.
Michelson dan Morley pada tahun 1887 dirancang percobaan, dengan menerapkan suatu interferometer dan cermin setengah perak, yang cukup akurat untuk mendeteksi aliran eter. Sistem cermin mencerminkan kembali cahaya ke interferometer. Jika ada sebuah drift eter, akan menghasilkan pergeseran fasa dan perubahan gangguan yang akan terdeteksi. Namun, tidak ada pergeseran fasa pernah ditemukan. Hasil negatif dari percobaan Michelson-Morley meninggalkan seluruh konsep eter tanpa alasan untuk ada. Lebih buruk lagi, itu menciptakan situasi membingungkan bahwa cahaya ternyata berperilaku seperti gelombang, namun media tanpa terdeteksi melalui aktivitas gelombang yang mungkin merambat.
Dalam sebuah makalah tahun 1964,Erik Christopher Zeeman menunjukkan bahwa kausalitas melestarikan properti, suatu kondisi yang lemah dalam arti matematis dari invarian dari kecepatan cahaya, sudah cukup untuk menjamin bahwa transformasi koordinat adalah transformasi Lorentz.

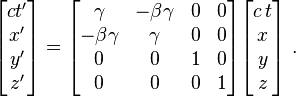
![L (\ mathbf {u}, U) L (\ mathbf {u}, V) = L (\ mathbf {u} \ U oplus \ mathbf {v}, gyr [\ mathbf {u}, U \ mathbf {v }] UV)](http://upload.wikimedia.org/math/d/9/6/d96b7609ddda2ec097ef9577b786eea7.png)





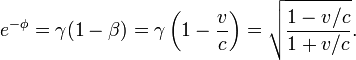
![\ Phi = \ ln \ left [\ gamma (1 + \ beta) \ right] = - \ ln \ left [\ gamma (1 - \ beta) \ right] \,](http://upload.wikimedia.org/math/4/0/5/4059316ea27f6c51c310306cc1753299.png)



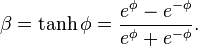
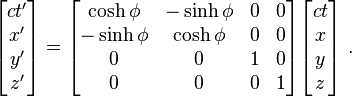
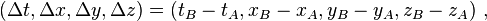
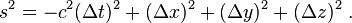
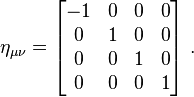
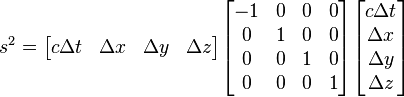
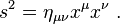
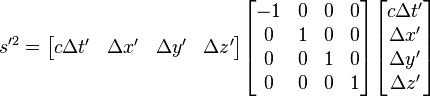
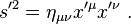


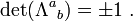






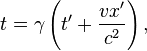
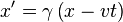









































0 komentar:
Posting Komentar